Càlcul de la força de flexió durant la flexió lliure de la màquina de flexió de xapa

En els darrers anys, les màquines plegadores de frens metàl·lics s'han utilitzat àmpliament en diverses indústries i la gamma de processament de màquines plegadores s'ha anat ampliant. Tanmateix, no hi ha hagut una discussió sistemàtica sobre el càlcul de la força de flexió. Actualment, hi ha aproximadament dos tipus de fórmules de càlcul de la força de flexió recomanades als manuals de diversos fabricants de màquines de flexió de premsa.

P - força de flexió, KN;

S - gruix de la làmina, mm;

l - la longitud de flexió de la làmina, m;

V - l'amplada de l'obertura de la matriu inferior, mm;

σb - Resistència a la tracció del material, MPa.

La taula de paràmetres de força de flexió recomanada pel fabricant també es calcula segons la fórmula anterior.

El procés de derivació i l'àmbit d'aplicació de la fórmula de càlcul de la força de flexió

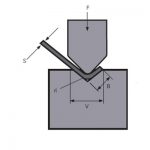
La figura 1 és un diagrama esquemàtic del treball durant el plegat de la làmina. A continuació es descriu el procés de derivació de la fórmula de càlcul de la força de flexió i dues condicions de paràmetre addicionals. En primer lloc, hi ha aquestes recomanacions al manual del producte. En plegat lliure, l'amplada d'obertura de matriu inferior seleccionada V és de 8 a 10 vegades el gruix de la làmina S. Aquí prenem la relació d'aspecte .

Figura 1 Diagrama esquemàtic de flexió

P - força de flexió

S - gruix de la làmina

V - ample inferior de l'obertura de la matriu

r - el radi interior quan es doblega la làmina

K - l'amplada de la projecció horitzontal de la zona de deformació de flexió=9

En segon lloc, el fabricant enumera els valors corresponents de l'amplada de la matriu V i el diàmetre interior r de la peça de flexió a la taula de paràmetres de la força de flexió. Generalment r=(0,16~0,17)V. Aquí, la relació diàmetre-amplada =0.16.

Durant el procés de flexió de la xapa, el material de la zona de deformació es troba en un estat de deformació altament plàstic i es doblega en un angle al voltant de la línia central. A la superfície exterior de la zona de flexió, en alguns casos poden aparèixer microesquerdes. A la secció transversal de la zona de deformació, excepte a la proximitat de la capa central, les tensions en altres punts són properes a la resistència a la tracció del material. La part superior de la capa neutra es comprimeix i la part inferior es tensa. La figura 2 mostra una secció transversal i el corresponent diagrama d'esforços a la zona de deformació.

Figura 2 Diagrama d'esforços

S - gruix de la làmina

l - longitud de flexió de la làmina

El moment flector a la secció transversal de la zona de deformació és:

El moment de flexió generat per la força de flexió de la màquina a la zona de deformació és (vegeu la figura 1):

Des de

Quan s'utilitzen motlles d'ús general per a la flexió lliure en una màquina dobladora, la major part de la xapa metàl·lica es doblega 90 °. Tal com es mostra a la figura 3. K és:

Substituint K a l'equació (1), obtenim:

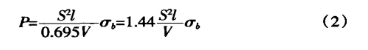
La resistència a la tracció dels materials ordinaris σb=450N/mm2, substituint la fórmula (2) per:

En el procés de derivació es pot veure que quan s'utilitza l'equació (2) o l'equació (3) per calcular la força de flexió, les dues

s'han de complir les condicions dels paràmetres esmentades anteriorment. És a dir, la relació d'aspecte=9, la relació diàmetre-amplada=0,16, en cas contrari, provocarà un gran error.

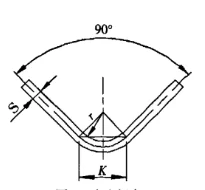
Figura 3 Flexió lliure

S - gruix de la làmina

r - el radi interior quan es doblega la làmina

K - l'amplada de la projecció horitzontal de la zona de deformació de flexió

Nous mètodes i passos per calcular la força de flexió

A causa dels requisits de disseny o de procés, de vegades és difícil complir els dos requisits addicionals anteriors al mateix temps. En aquest moment, la fórmula de càlcul recomanada no s'ha d'utilitzar per calcular la força de flexió, sinó que s'ha de dur a terme segons els passos següents.

(1) Segons el gruix de la placa S, el radi de flexió r i l'obertura inferior de la matriu V, es calculen respectivament la relació entre l'amplada i el gruix i la relació diàmetre i amplada.

(2) Calculeu l'amplada de projecció de la zona de deformació segons la deformació de la làmina.

(3) Apliqueu la fórmula (1) per calcular la força de flexió.

En el procés de càlcul, s'ha considerat la diferència del radi de flexió i el canvi de la zona de deformació corresponent. La força de flexió calculada a partir d'això és més precisa i fiable que el resultat calculat per la fórmula habitualment recomanada. Ara doneu un exemple per il·lustrar, tal com es mostra a la figura 4.

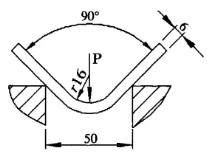
Figura 4 Nou mètode de càlcul

Conegut: el gruix de la làmina S = 6 mm, la longitud de la làmina l = 4 m, el radi de flexió r = 16 mm, l'amplada d'obertura de la matriu inferior V = 50 mm i la resistència a la tracció del material σb = 450 N/mm2. Trobeu la força de flexió necessària per a la flexió lliure.

Primer, cerqueu la relació d'aspecte i la relació diàmetre-amplada:

En segon lloc, calculeu l'amplada de projecció de la zona de deformació:

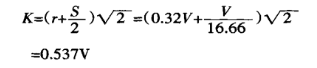
Finalment, utilitzeu l'equació (1) per trobar la força de flexió:

Si s'utilitza la fórmula habitual recomanada per calcular la força de flexió:

Des de = 1,5, es pot veure que la diferència entre ambdós és 1,5 vegades. El motiu d'aquest error és que el radi de flexió en aquest exemple és relativament gran i l'àrea de deformació corresponent augmenta, de manera que es requereix una força de flexió més gran durant la flexió. En aquest exemple, la relació diàmetre-amplada=0,32, que ha superat les condicions addicionals dels paràmetres introduïts anteriorment. Òbviament, és inadequat utilitzar la fórmula habitualment recomanada per calcular la força de flexió. Podeu veure els avantatges del nou mètode de càlcul en aquest exemple.

Conclusió

Els passos i fórmules per calcular la força de flexió que s'introdueixen aquí no només són aplicables a la flexió d'angle de la xapa, sinó també a la flexió de l'arc (en sentit estricte, s'hauria d'anomenar flexió d'angle amb un radi de flexió extragran). Cal assenyalar que la forma del motlle és especial quan la làmina es doblega en forma d'arc. En calcular la projecció de la zona de deformació, s'ha de calcular d'acord amb els paràmetres tecnològics establerts en el procés tecnològic, que no es poden expressar amb una fórmula simple.

Quan es dissenya un motlle en forma d'arc, utilitzant el mètode introduït en aquest article per calcular la força de flexió, es poden obtenir resultats satisfactoris.